Least Common Multiple Of 6 And 9
xcpfox
Nov 14, 2025 · 12 min read
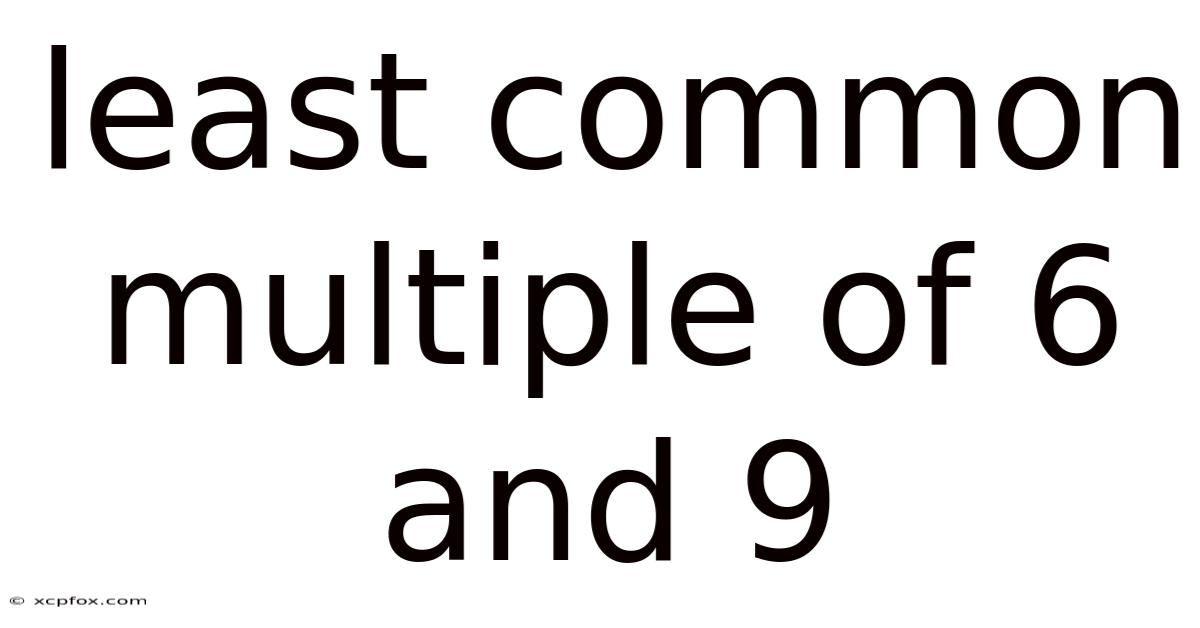
Table of Contents
Imagine you're organizing a school event. You want to buy snacks, with one type sold in packs of 6 and another in packs of 9. To ensure you have an equal number of both snacks and minimize waste, you need to find the smallest number of snacks that can be bought in both pack sizes. This is where the concept of the least common multiple comes into play.
The least common multiple (LCM) of 6 and 9 is a fundamental concept in mathematics that helps us understand how numbers relate to each other. Finding the LCM isn't just an abstract exercise; it has practical applications in various fields, from everyday problem-solving to advanced mathematical computations. This article will delve into the LCM of 6 and 9, exploring its definition, methods for calculation, real-world applications, and some interesting facts.
Unveiling the Least Common Multiple: A Detailed Overview
The least common multiple (LCM) of two or more numbers is the smallest positive integer that is perfectly divisible by each of those numbers. In simpler terms, it’s the smallest number that all the given numbers can divide into without leaving a remainder. Understanding the LCM is crucial in many areas of mathematics, including fractions, algebra, and number theory.
To truly grasp the significance of the LCM, it's important to differentiate it from the greatest common divisor (GCD), also known as the highest common factor (HCF). While the LCM is the smallest multiple that two numbers share, the GCD is the largest factor that both numbers have in common. The LCM and GCD are related through a simple formula: LCM(a, b) * GCD(a, b) = |a * b|. This relationship highlights the interconnectedness of these two fundamental concepts in number theory.
Historically, the concept of LCM can be traced back to ancient civilizations. The need to solve problems related to dividing quantities and understanding cyclical events led to the development of methods for finding the LCM. Ancient mathematicians in Egypt, Greece, and India developed techniques for finding common multiples, which were essential for astronomical calculations, calendar construction, and fair distribution of resources. Over time, these methods evolved into the more formal and efficient algorithms we use today.
The LCM is built upon the foundation of prime numbers. A prime number is a number greater than 1 that has no positive divisors other than 1 and itself. Understanding the prime factorization of numbers is essential for finding the LCM. Every integer greater than 1 can be uniquely expressed as a product of prime numbers. For example, the prime factorization of 6 is 2 x 3, and the prime factorization of 9 is 3 x 3 (or 3^2). These prime factorizations are the building blocks for determining the LCM.
The importance of the LCM extends beyond theoretical mathematics. In practical applications, the LCM is used in various fields, such as scheduling, engineering, and computer science. Understanding how to calculate and apply the LCM can lead to more efficient solutions and better decision-making in many real-world scenarios. For example, in scheduling, the LCM helps determine when events will coincide, and in engineering, it is used to synchronize machines or processes.
Comprehensive Exploration of LCM(6, 9)
The least common multiple of 6 and 9 is the smallest number that both 6 and 9 divide into evenly. Let's break down how to find this value using different methods.
One of the simplest ways to find the LCM is by listing the multiples of each number until you find a common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, ...
- Multiples of 9: 9, 18, 27, 36, 45, ...
By comparing the lists, we can see that the smallest number that appears in both lists is 18. Therefore, the LCM of 6 and 9 is 18. This method is straightforward and easy to understand, especially for smaller numbers, but it can become cumbersome for larger numbers.
Another method involves finding the prime factorization of each number:
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3 x 3 (or 3^2)
To find the LCM, take the highest power of each prime factor that appears in either factorization:
- The highest power of 2 is 2^1 (from the factorization of 6).
- The highest power of 3 is 3^2 (from the factorization of 9).
Multiply these highest powers together: LCM(6, 9) = 2^1 x 3^2 = 2 x 9 = 18. This method is more efficient for larger numbers because it breaks the problem down into smaller, more manageable steps.
Using the formula LCM(a, b) * GCD(a, b) = |a * b|, we first need to find the greatest common divisor (GCD) of 6 and 9. The GCD is the largest number that divides both 6 and 9.
- Factors of 6: 1, 2, 3, 6
- Factors of 9: 1, 3, 9
The largest number that appears in both lists is 3, so GCD(6, 9) = 3.
Now we can use the formula: LCM(6, 9) * 3 = |6 * 9| LCM(6, 9) * 3 = 54 LCM(6, 9) = 54 / 3 = 18
Thus, the LCM of 6 and 9 is 18. This method is particularly useful when you already know the GCD of the numbers.
When dealing with multiple numbers, the same principles apply. For example, to find the LCM of 6, 9, and 12:
- Prime factorization of 6: 2 x 3
- Prime factorization of 9: 3^2
- Prime factorization of 12: 2^2 x 3
Take the highest power of each prime factor:
- Highest power of 2: 2^2
- Highest power of 3: 3^2
Multiply these together: LCM(6, 9, 12) = 2^2 x 3^2 = 4 x 9 = 36.
Understanding the LCM of 6 and 9 is not just a mathematical exercise; it has several practical applications. Consider the scenario of scheduling events. If one event occurs every 6 days and another event occurs every 9 days, the LCM (18) tells you that both events will coincide every 18 days. This concept is crucial in various fields, from project management to manufacturing.
Current Trends and Developments in LCM Applications
The use of the least common multiple continues to evolve with advancements in technology and mathematics. One notable trend is the integration of LCM calculations in software and algorithms used for optimization and scheduling. For instance, in supply chain management, the LCM helps in synchronizing different processes to minimize delays and inefficiencies.
Data analysis also plays a significant role in the application of LCM. By analyzing data sets, professionals can identify patterns and cycles that require synchronization. This is particularly useful in industries such as transportation, where schedules need to be optimized to reduce congestion and improve service reliability. Modern algorithms leverage computing power to handle larger and more complex data sets, making LCM calculations more efficient and applicable to a wider range of problems.
In education, there is a growing emphasis on teaching LCM through interactive and visual methods. Traditional approaches often rely on rote memorization, but educators are now incorporating games, simulations, and real-world examples to make the concept more accessible and engaging for students. This shift towards more intuitive teaching methods helps students grasp the underlying principles of LCM and apply them effectively in problem-solving.
Another trend is the increasing use of LCM in cryptography and data encryption. While not a direct application, the principles of number theory, including LCM, are fundamental to many encryption algorithms. Understanding LCM and related concepts helps in developing more secure and efficient encryption methods, which are crucial in protecting sensitive data in the digital age.
The application of LCM in renewable energy is also gaining traction. For example, in the design of solar panel systems, LCM can be used to optimize the arrangement of panels to maximize energy capture and minimize shading. Similarly, in wind energy, LCM can help synchronize the operation of multiple turbines to improve overall energy production. These applications demonstrate the versatility of LCM in addressing modern challenges.
Furthermore, the least common multiple is finding new applications in the field of artificial intelligence (AI). AI algorithms often need to solve complex optimization problems, and LCM can be a useful tool in identifying repeating patterns and cycles. By incorporating LCM calculations into AI models, researchers can develop more efficient and robust solutions for various applications, such as robotics, machine learning, and natural language processing.
Tips and Expert Advice for Mastering LCM
Mastering the concept of the least common multiple requires a combination of understanding the underlying principles and applying practical techniques. Here are some expert tips to help you improve your skills and tackle LCM problems effectively.
First, always start with a clear understanding of the definition of LCM. Remember that the LCM is the smallest positive integer that is divisible by all the given numbers. This fundamental understanding will guide your approach to solving problems and prevent common mistakes. Make sure you also grasp the difference between LCM and GCD, as they are often used together in various mathematical contexts.
Practice different methods for finding the LCM. As discussed earlier, there are several methods, including listing multiples, prime factorization, and using the GCD. Experiment with each method and identify which one works best for you in different situations. For smaller numbers, listing multiples might be the quickest approach, while prime factorization is more efficient for larger numbers. Familiarity with multiple methods will make you a more versatile problem solver.
Use real-world examples to reinforce your understanding. Look for opportunities to apply LCM in everyday situations. For example, if you are planning a schedule with recurring tasks, use the LCM to determine when those tasks will coincide. The more you apply the concept in practical scenarios, the better you will understand its significance and utility.
When dealing with larger numbers, prime factorization is your best friend. Break down each number into its prime factors and then identify the highest power of each prime factor. Multiplying these highest powers together will give you the LCM. This method is not only efficient but also reduces the risk of errors, especially when compared to listing multiples of large numbers.
Consider using online calculators and tools to verify your answers. There are many free LCM calculators available online that can help you check your work and gain confidence in your calculations. However, be sure to use these tools as a supplement to your learning, not as a replacement for understanding the underlying concepts. Always try to solve the problem yourself first and then use the calculator to verify your answer.
Another useful tip is to look for patterns and shortcuts. For example, if one of the numbers is a multiple of the other, then the larger number is the LCM. Similarly, if the numbers are relatively prime (i.e., their GCD is 1), then the LCM is simply the product of the numbers. Recognizing these patterns can save you time and effort when solving problems.
Finally, don't be afraid to ask for help. If you are struggling with LCM, reach out to teachers, classmates, or online communities for assistance. Explaining your difficulties and listening to different perspectives can help you gain a deeper understanding of the concept and overcome any challenges you may be facing. Remember, learning is a collaborative process, and seeking help is a sign of strength, not weakness.
Frequently Asked Questions about LCM(6, 9)
Q: What is the least common multiple (LCM)? A: The least common multiple (LCM) of two or more numbers is the smallest positive integer that is divisible by each of those numbers without leaving a remainder.
Q: How do you find the LCM of 6 and 9? A: There are several methods: listing multiples, prime factorization, or using the formula LCM(a, b) = |a * b| / GCD(a, b). All methods will yield LCM(6, 9) = 18.
Q: Why is the LCM important? A: The LCM is important in various mathematical applications, such as simplifying fractions, scheduling events, and solving problems involving repeating cycles.
Q: Can the LCM be larger than the numbers you're finding it for? A: Yes, the LCM is always greater than or equal to the largest number in the set. In the case of 6 and 9, the LCM is 18, which is larger than both 6 and 9.
Q: What is the difference between LCM and GCD? A: The LCM is the smallest multiple that two numbers share, while the GCD (greatest common divisor) is the largest factor that both numbers have in common.
Q: Is there a formula to calculate the LCM using the GCD? A: Yes, the formula is LCM(a, b) * GCD(a, b) = |a * b|. This formula relates the LCM and GCD, making it easier to calculate one if you know the other.
Q: How is the LCM used in real-world applications? A: The LCM is used in scheduling, engineering, and computer science. For example, it can help determine when events will coincide or synchronize machines in a factory.
Q: What is the LCM of 6, 9, and 12? A: The LCM of 6, 9, and 12 is 36. This can be found using prime factorization or listing multiples.
Q: Can the LCM be a negative number? A: By definition, the LCM is always a positive integer. While negative multiples exist, the least common multiple refers specifically to the smallest positive multiple.
Q: What if the numbers have no common factors other than 1? A: If the numbers have no common factors other than 1 (i.e., they are relatively prime), the LCM is simply the product of the numbers. For example, the LCM of 5 and 7 is 35.
Conclusion
In summary, the least common multiple of 6 and 9 is 18. This concept is a cornerstone of number theory and has practical applications in various fields. Understanding the different methods for finding the LCM, such as listing multiples, prime factorization, and using the GCD, is essential for mastering this concept.
Whether you're a student learning the basics or a professional applying these concepts in your work, a solid understanding of LCM will undoubtedly enhance your problem-solving skills. Continue exploring and practicing to deepen your knowledge and discover new applications of this fundamental mathematical idea.
If you found this article helpful, please share it with others who might benefit from understanding the LCM. Do you have any questions or insights about the LCM of 6 and 9? Leave a comment below and let's discuss!
Latest Posts
Latest Posts
-
Elon Musk Net Worth In Rupees
Nov 14, 2025
-
What Is A Negative Minus A Negative
Nov 14, 2025
-
What Is Dividend Divisor And Quotient
Nov 14, 2025
-
Can I Grow A Mango Tree From A Seed
Nov 14, 2025
-
What Are The 3 Parts Of A Comet
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 6 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.