Least Common Multiple Of 4 And 6
xcpfox
Nov 10, 2025 · 11 min read
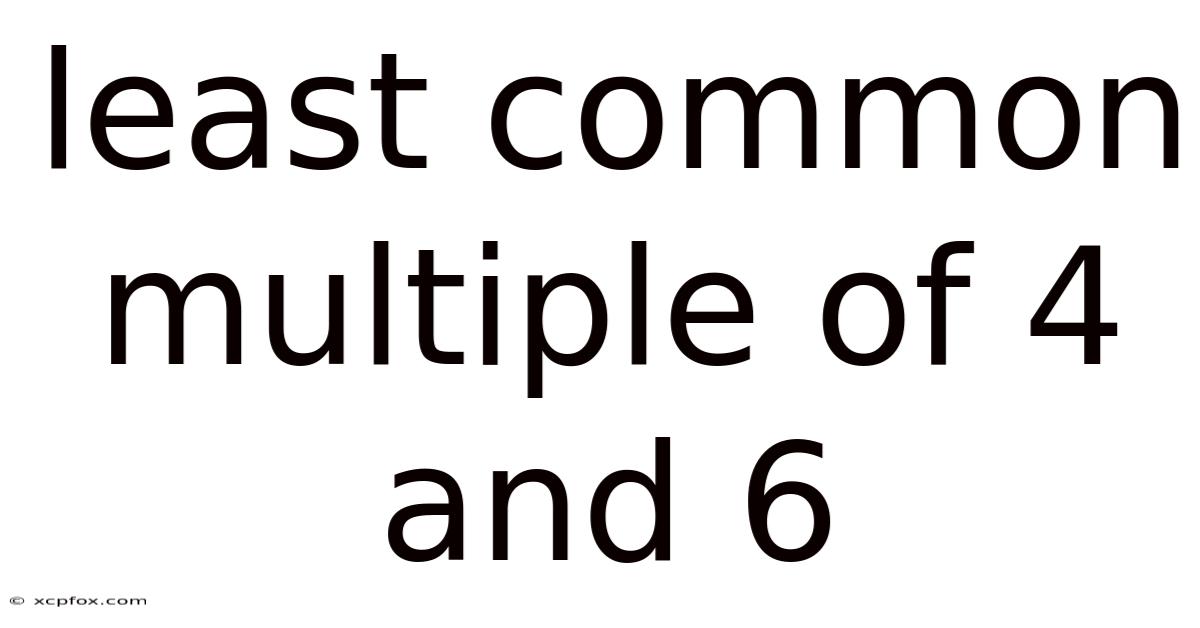
Table of Contents
Imagine you're planning a small party. You want to serve both hotdogs and hamburgers. Hotdog buns come in packs of 4, and hamburger buns come in packs of 6. You don't want any buns left over. What's the smallest number of each you need to buy so that you have an equal number of hotdogs and hamburgers? This seemingly simple question introduces us to the concept of the least common multiple, or LCM.
Now, picture this: you are a city planner tasked with synchronizing two different traffic lights. One light changes every 4 seconds, and the other changes every 6 seconds. You need to figure out when they will both change at the exact same time to optimize traffic flow. Understanding the least common multiple (LCM) of 4 and 6 is crucial to solving this problem. In this article, we'll dive deep into the world of LCM, explore its practical applications, and understand why it's a fundamental concept in mathematics. So, let’s find out what exactly is the least common multiple of 4 and 6.
Main Subheading: Understanding the Least Common Multiple (LCM)
The least common multiple (LCM), also known as the lowest common multiple or smallest common multiple, is a foundational concept in number theory. It is the smallest positive integer that is divisible by both numbers without leaving a remainder. This concept applies to any set of numbers, but we will focus primarily on the LCM of two numbers, particularly 4 and 6.
Understanding the LCM is not merely an academic exercise. It has real-world applications across various fields, including scheduling, engineering, and computer science. Whether you're coordinating events, designing mechanical systems, or writing algorithms, the LCM helps in synchronizing and optimizing processes. In simple terms, the LCM helps us find the smallest number that two or more numbers can divide into evenly.
Comprehensive Overview: Diving Deep into LCM
To truly grasp the significance of the least common multiple, we need to explore its formal definition, underlying mathematical principles, and historical context. This section provides an in-depth look at the concept of LCM.
Definition of Least Common Multiple
The least common multiple (LCM) of two or more integers a and b is the smallest positive integer that is a multiple of both a and b. In other words, it is the smallest number that both a and b divide into evenly.
For example, consider the numbers 4 and 6. Multiples of 4 are 4, 8, 12, 16, 20, 24, and so on. Multiples of 6 are 6, 12, 18, 24, 30, and so on. The common multiples of 4 and 6 are 12, 24, 36, and so on. The smallest of these common multiples is 12. Therefore, the LCM of 4 and 6 is 12.
Mathematical Foundation
The concept of LCM is closely tied to the greatest common divisor (GCD). The GCD of two numbers is the largest positive integer that divides both numbers without leaving a remainder. There is a fundamental relationship between the LCM and GCD:
LCM(a, b) = |a * b| / GCD(a, b)
This formula tells us that the LCM of two numbers can be found by multiplying the numbers together and then dividing by their GCD.
For example, to find the LCM of 4 and 6, we first find the GCD of 4 and 6. The factors of 4 are 1, 2, and 4. The factors of 6 are 1, 2, 3, and 6. The greatest common factor is 2. Thus, GCD(4, 6) = 2.
Using the formula: LCM(4, 6) = |4 * 6| / GCD(4, 6) = 24 / 2 = 12
This confirms that the LCM of 4 and 6 is indeed 12.
Historical Context and Evolution
The concept of LCM has ancient roots, tracing back to early civilizations that dealt with problems involving proportions and ratios. Ancient mathematicians in Greece, particularly those associated with the Pythagorean school, explored number theory extensively, including concepts related to multiples and divisors.
Euclid's Elements, written around 300 BC, contains many foundational theorems related to number theory, although it does not explicitly define the LCM. However, the principles and methods described in Elements laid the groundwork for understanding and calculating LCM.
In ancient China, mathematicians also studied LCM in the context of calendar calculations and astronomical observations. The Sunzi Suanjing, a mathematical text from the 3rd to 5th centuries AD, includes problems involving common multiples.
Over time, mathematicians developed more efficient methods for calculating the LCM, particularly with the rise of algebra and more sophisticated number theory. Today, the LCM is a standard topic in elementary number theory and is taught in schools worldwide.
Methods to Calculate LCM
There are several methods to calculate the LCM of two or more numbers. Here are the most common methods:
-
Listing Multiples: This method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
- Multiples of 4: 4, 8, 12, 16, 20, 24, ...
- Multiples of 6: 6, 12, 18, 24, 30, ...
In this case, the LCM of 4 and 6 is 12.
-
Prime Factorization: This method involves finding the prime factorization of each number and then taking the highest power of each prime factor that appears in any of the factorizations.
- Prime factorization of 4: 2^2
- Prime factorization of 6: 2 * 3
LCM(4, 6) = 2^2 * 3 = 4 * 3 = 12
-
Using the GCD: As mentioned earlier, the LCM can be calculated using the formula:
LCM(a, b) = |a * b| / GCD(a, b)
We found that GCD(4, 6) = 2. Therefore, LCM(4, 6) = (4 * 6) / 2 = 24 / 2 = 12.
-
Division Method: This method involves dividing the numbers by their common prime factors until all the quotients are 1. The LCM is the product of the divisors.
4 6 2 2 3 2 1 3 3 1 1 LCM(4, 6) = 2 * 2 * 3 = 12
Why LCM of 4 and 6 is 12
To reiterate, the LCM of 4 and 6 is 12 because 12 is the smallest positive integer that is divisible by both 4 and 6 without leaving a remainder. This can be confirmed through listing multiples, prime factorization, using the GCD, or the division method. The practical applications of this simple calculation are vast and varied, from coordinating events to optimizing engineering designs.
Trends and Latest Developments
While the concept of LCM is well-established, its application and relevance continue to evolve with technological advancements and changing societal needs. Here are some trends and latest developments related to LCM:
Computational Tools and Algorithms
With the advent of powerful computing tools, calculating the LCM of large numbers has become significantly easier. Various software programs and online calculators can quickly determine the LCM of any set of numbers.
Moreover, algorithmic optimizations have improved the efficiency of LCM calculations, particularly in computer science applications. Algorithms like the Euclidean algorithm, used to find the GCD, have been refined to enhance the speed and accuracy of LCM computations.
Interdisciplinary Applications
The application of LCM extends beyond traditional mathematics into diverse fields. For instance, in computer science, LCM is used in scheduling tasks, optimizing memory allocation, and synchronizing processes. In engineering, it is applied in designing gears, synchronizing machines, and planning construction projects.
In music theory, LCM is used to understand rhythmic patterns and harmonies. By finding the LCM of different musical intervals, musicians can create complex and interesting compositions.
Educational Approaches
Modern educational approaches emphasize the practical relevance of LCM to enhance student engagement and understanding. Instead of rote memorization, educators focus on real-world examples and interactive activities that demonstrate the utility of LCM.
For example, teachers might use scenarios like planning a party, coordinating events, or designing traffic light systems to illustrate the importance of LCM. These hands-on activities help students grasp the concept and appreciate its applications.
Data Analysis and LCM
In data analysis, the concept of LCM can be applied in time series analysis and synchronization of events. For example, when analyzing periodic events that occur at different intervals, finding the LCM of those intervals can help identify patterns and predict future occurrences.
Professional Insights
Experts in mathematics and related fields emphasize the importance of understanding LCM as a fundamental building block for more advanced concepts. A solid grasp of LCM can enhance problem-solving skills and improve analytical thinking.
"Understanding LCM is crucial for anyone working with numbers, whether in mathematics, engineering, or computer science," says Dr. Emily Carter, a professor of mathematics. "It provides a foundation for understanding more complex concepts and solving real-world problems."
Tips and Expert Advice
Understanding the LCM and applying it effectively requires not just theoretical knowledge but also practical skills. Here are some tips and expert advice to help you master the concept:
Master the Basics
Before diving into complex applications, ensure you have a solid understanding of the basic definition and methods for calculating the LCM. Practice with simple examples to build confidence and familiarity.
Start with small numbers like 2, 3, 4, 5, and 6. Use the listing multiples method, prime factorization, and the GCD method to calculate their LCMs. This practice will help you understand the underlying principles and develop a strong foundation.
Relate to Real-World Examples
One of the best ways to understand LCM is to relate it to real-world examples. Think about situations where you need to synchronize events or coordinate schedules.
For example, consider a scenario where you have two tasks: Task A needs to be completed every 4 days, and Task B needs to be completed every 6 days. When will both tasks need to be completed on the same day? The answer is the LCM of 4 and 6, which is 12. So, every 12 days, both tasks will coincide.
Use Visual Aids
Visual aids can be incredibly helpful in understanding and applying the concept of LCM. Diagrams, charts, and interactive tools can make the process more intuitive and engaging.
For example, create a number line and mark the multiples of 4 and 6. You’ll quickly see that the first common multiple is 12. This visual representation can help reinforce the concept and make it easier to remember.
Practice Regularly
Like any skill, mastering LCM requires regular practice. Solve a variety of problems, ranging from simple calculations to more complex applications.
Look for practice problems online or in textbooks. Challenge yourself with increasingly difficult questions to test your understanding and improve your problem-solving skills.
Understand the Connection to GCD
The relationship between LCM and GCD is fundamental. Make sure you understand how to calculate the GCD and how it relates to the LCM.
Use the formula LCM(a, b) = |a * b| / GCD(a, b) to reinforce the connection. Practice finding both the GCD and LCM for different pairs of numbers to solidify your understanding.
Utilize Technology
Take advantage of the various computational tools and online calculators available. These tools can help you quickly calculate the LCM of large numbers and check your work.
However, be sure to understand the underlying principles and methods. Don't rely solely on technology without understanding the math behind it.
Seek Expert Guidance
If you're struggling to understand LCM, don't hesitate to seek guidance from teachers, tutors, or online resources. Expert advice can provide clarity and help you overcome challenges.
Join online forums or discussion groups where you can ask questions and learn from others. Participate in study groups or workshops to enhance your understanding and skills.
FAQ
Q: What is the difference between LCM and GCD? A: The least common multiple (LCM) is the smallest number that two or more numbers can divide into evenly, while the greatest common divisor (GCD) is the largest number that divides two or more numbers evenly.
Q: How do you find the LCM of more than two numbers? A: To find the LCM of more than two numbers, you can use the prime factorization method or find the LCM of the first two numbers, then find the LCM of that result with the next number, and so on.
Q: Is LCM always greater than or equal to the numbers? A: Yes, the LCM is always greater than or equal to the largest of the numbers because it must be a multiple of all the numbers.
Q: Can LCM be zero? A: No, the LCM is always a positive integer. Zero is a multiple of every number, but it is not considered the least common multiple.
Q: Why is LCM important? A: LCM is important because it helps in solving problems involving synchronization, scheduling, and coordination in various fields such as mathematics, engineering, and computer science.
Conclusion
Understanding the least common multiple (LCM) of 4 and 6, which is 12, is more than just an academic exercise. It is a gateway to understanding broader mathematical principles and their applications in the real world. From coordinating events to optimizing complex systems, the LCM provides a foundation for solving a wide range of problems.
By mastering the basics, relating to real-world examples, and practicing regularly, you can develop a strong understanding of LCM and its significance. Whether you're a student, engineer, or simply someone who enjoys problem-solving, the knowledge of LCM can be a valuable asset. Explore further, practice, and deepen your understanding of LCM and its related concepts. Engage with online resources, participate in discussions, and continue to apply your knowledge in practical scenarios. Start exploring the fascinating world of number theory today!
Latest Posts
Latest Posts
-
What Is 90 Days From 11 15 24
Nov 10, 2025
-
How Many Seconds Ar Ein An Hour
Nov 10, 2025
-
Is Neptune Bigger Or Smaller Than Earth
Nov 10, 2025
-
Rules For Odd And Even Functions
Nov 10, 2025
-
How To Find Perimeter Of A Figure
Nov 10, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.