E Equals Mc Squared Solve For M
xcpfox
Nov 12, 2025 · 10 min read
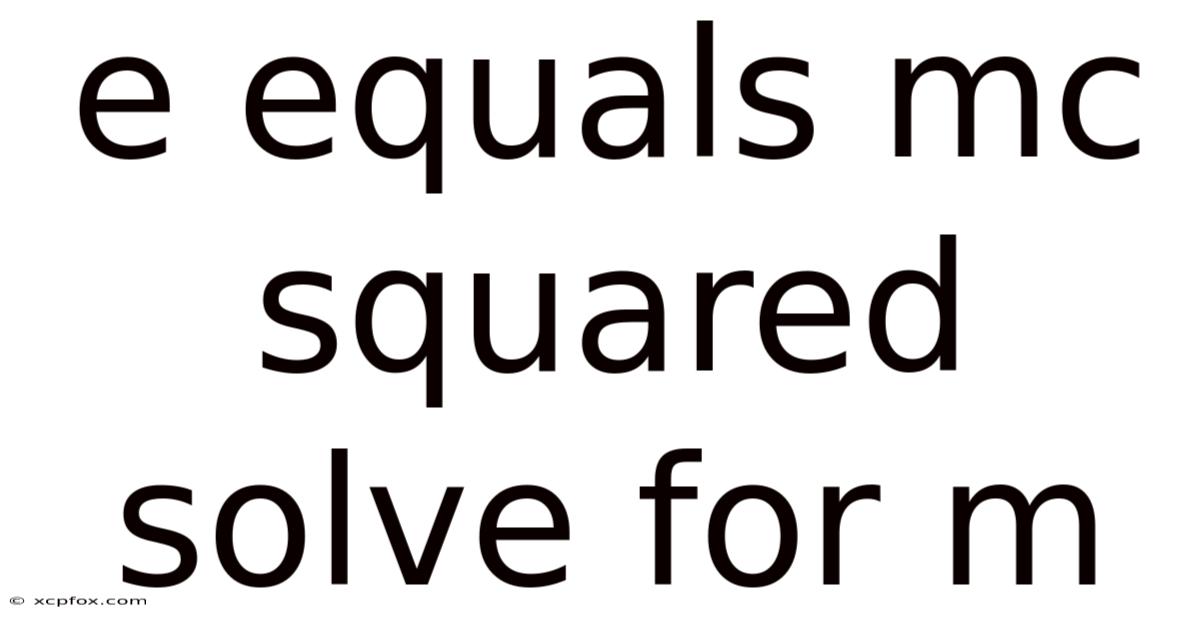
Table of Contents
Imagine holding a tiny pebble, seemingly insignificant, yet containing within it an unimaginable amount of energy. This is the essence of Einstein's famous equation, E=mc², a cornerstone of modern physics that elegantly connects energy and mass. For many, it's just a catchy phrase, but nestled within those three symbols lies a profound understanding of the universe.
Perhaps you've stumbled upon this equation and wondered about its practical applications. Or maybe you're a student grappling with its implications in a physics problem. Whatever your reason, understanding how to manipulate this equation, specifically to solve for mass (m), unlocks a deeper appreciation for the relationship between matter and energy. Let's embark on a journey to demystify E=mc², explore its significance, and learn how to rearrange it to find the elusive 'm'.
Main Subheading: Unveiling E=mc²
E=mc² isn't just a random assortment of letters and numbers; it's a powerful statement about the fundamental nature of reality. It succinctly describes the equivalence of energy and mass, asserting that energy (E) is equal to mass (m) multiplied by the speed of light (c) squared. This equation, derived by Albert Einstein as part of his theory of special relativity, revolutionized our understanding of physics, particularly at extreme speeds and energies.
The beauty of E=mc² lies in its simplicity. It reveals that mass and energy are interchangeable; one can be converted into the other. This concept is at the heart of nuclear reactions, where a small amount of mass can be converted into a tremendous amount of energy, as seen in nuclear power plants and, unfortunately, in atomic weapons. Conversely, energy can also be converted into mass, a phenomenon observed in particle accelerators where high-energy collisions can create new, heavier particles.
Comprehensive Overview
To truly grasp the power of E=mc², let's delve into its components and their significance:
-
E: Energy. Measured in joules (J), energy represents the capacity to do work. It can exist in various forms, such as kinetic energy (energy of motion), potential energy (stored energy), thermal energy (heat), and electromagnetic energy (light). In the context of E=mc², E refers to the total energy equivalent to the mass, including its rest energy.
-
m: Mass. Typically measured in kilograms (kg), mass is a measure of an object's resistance to acceleration. In simpler terms, it's a measure of how much "stuff" is in an object. It's crucial to understand that in relativity, mass is not always constant. The 'm' in E=mc² specifically refers to the relativistic mass which increases with velocity. However, when dealing with objects at everyday speeds, the difference between relativistic mass and rest mass (the mass of an object when it's at rest) is negligible. In most common applications of E=mc², we are concerned with rest mass.
-
c: The Speed of Light. A universal constant, the speed of light in a vacuum is approximately 299,792,458 meters per second (m/s). Represented by 'c', it's a fundamental limit on the speed at which information or energy can travel. The fact that it's squared in the equation highlights the immense amount of energy contained within even a small amount of mass. Squaring such a large number results in an even larger number, demonstrating that a tiny amount of mass can be converted into a colossal amount of energy.
The equation itself stems from Einstein's theory of special relativity, which postulates that the laws of physics are the same for all observers in uniform motion relative to one another, and that the speed of light in a vacuum is the same for all observers, regardless of the motion of the light source. This seemingly simple statement has profound consequences, leading to concepts like time dilation and length contraction, and ultimately culminating in the mass-energy equivalence expressed by E=mc².
The historical context is also crucial. Before Einstein, mass and energy were considered separate and conserved quantities. The law of conservation of mass stated that mass cannot be created or destroyed, only transformed. Similarly, the law of conservation of energy stated that energy cannot be created or destroyed, only converted from one form to another. Einstein's equation shattered this paradigm, demonstrating that mass and energy are simply different forms of the same thing, and that the total amount of mass-energy in the universe is conserved. This understanding paved the way for the development of nuclear technology and our understanding of stellar processes.
The implications of E=mc² extend far beyond nuclear physics. It's fundamental to understanding the behavior of stars, where nuclear fusion converts mass into energy, powering their luminosity. It also plays a role in understanding the Big Bang and the formation of the universe. The equation continues to be a cornerstone of research in high-energy physics, particle physics, and cosmology.
Trends and Latest Developments
The ongoing exploration of E=mc² continues to drive innovation and deepen our understanding of the universe. One area of active research involves exploring the limits of the equation itself. While E=mc² is incredibly accurate under a wide range of conditions, physicists are constantly probing for potential deviations or limitations, especially at extremely high energies or gravitational fields.
Another area of interest is the practical application of mass-energy conversion. While nuclear power plants currently utilize this principle, researchers are exploring more efficient and sustainable methods of energy production based on nuclear fusion or other exotic processes. The development of controlled fusion, which mimics the energy production of the sun, remains a major goal in the quest for clean and abundant energy.
Furthermore, the equation plays a vital role in understanding the nature of dark matter and dark energy, which make up the vast majority of the universe's mass-energy content. While we don't yet fully understand what these mysterious substances are, E=mc² provides a framework for exploring their properties and interactions.
Data from particle accelerators like the Large Hadron Collider (LHC) continues to provide valuable insights into the fundamental particles and forces that govern the universe. By smashing particles together at near-light speeds, physicists can create new particles and study their properties, furthering our understanding of mass-energy conversion at the most fundamental level.
From a popular perspective, there's a growing awareness of the implications of E=mc² for space travel. The concept of converting matter directly into energy could potentially revolutionize space propulsion, enabling faster and more efficient travel to distant stars. While the technology for such advanced propulsion systems is still far off, the theoretical foundation is rooted in Einstein's famous equation.
Tips and Expert Advice
Now, let's get practical. How do we actually solve E=mc² for 'm'? Here's a step-by-step guide:
-
Start with the equation: E = mc²
-
Isolate 'm': To get 'm' by itself, we need to divide both sides of the equation by c².
-
Perform the division: Dividing both sides by c² gives us: E / c² = (mc²) / c²
-
Simplify: The c² on the right side of the equation cancels out, leaving us with: E / c² = m
-
Rewrite for clarity: Finally, we can rewrite the equation as: m = E / c²
So, to find the mass (m), you simply divide the energy (E) by the speed of light squared (c²). Remember to use consistent units; joules for energy, kilograms for mass, and meters per second for the speed of light.
Let's look at a real-world example. Suppose we want to find the mass equivalent of 4.5 x 10^14 Joules of energy (approximately the energy released by detonating one kiloton of TNT).
-
Identify the knowns: E = 4.5 x 10^14 J, c = 299,792,458 m/s
-
Apply the formula: m = E / c²
-
Substitute the values: m = (4.5 x 10^14 J) / (299,792,458 m/s)²
-
Calculate c²: c² ≈ 8.988 x 10^16 m²/s²
-
Calculate m: m ≈ (4.5 x 10^14 J) / (8.988 x 10^16 m²/s²) ≈ 0.005 kg
Therefore, the mass equivalent of 4.5 x 10^14 Joules of energy is approximately 0.005 kilograms, or 5 grams. This seemingly small amount of mass can unleash a tremendous amount of energy, illustrating the power of E=mc².
When working with E=mc², it's important to be mindful of the units. In physics, using the correct units is essential for obtaining accurate results. Always convert all values to SI units (meters, kilograms, seconds, joules) before plugging them into the equation. Also, remember that this equation applies in the context of special relativity, which deals with objects moving at constant velocities in a straight line. For situations involving acceleration or gravity, more complex equations from general relativity may be required.
Another crucial aspect is understanding the difference between energy released and energy converted. In many scenarios, only a fraction of the mass is converted into energy. For example, in a nuclear reaction, not all of the mass of the reactants is converted into energy; some of it remains in the products. To calculate the energy released, you need to determine the mass defect, which is the difference between the mass of the reactants and the mass of the products. This mass defect is then used in the E=mc² equation to calculate the energy released.
FAQ
Q: What does E=mc² mean in simple terms?
A: It means that energy and mass are two forms of the same thing, and a small amount of mass can be converted into a large amount of energy, and vice versa.
Q: Is E=mc² used in everyday life?
A: While you might not directly calculate it daily, E=mc² is fundamental to technologies like nuclear power and medical imaging (PET scans). It also helps us understand the sun's energy production.
Q: Can I really turn anything into energy using E=mc²?
A: In theory, yes. However, in practice, converting matter into energy requires extreme conditions like those found in nuclear reactions or particle accelerators.
Q: What are the units for each variable in E=mc² when solving for 'm'?
A: E (energy) is measured in joules (J), c (speed of light) is measured in meters per second (m/s), and m (mass) will be in kilograms (kg).
Q: Does the equation E=mc² have any limitations?
A: Yes, it's primarily applicable in the context of special relativity, dealing with constant velocities. General relativity is needed for scenarios involving gravity or acceleration. Also, it does not account for potential energy.
Conclusion
Einstein's E=mc² is more than just an equation; it's a gateway to understanding the fundamental relationship between energy and mass. By understanding how to solve for mass (m = E / c²), you gain a powerful tool for exploring the universe, from the smallest subatomic particles to the largest celestial bodies. This simple equation unlocks profound insights into nuclear reactions, stellar processes, and the very fabric of reality.
Now that you understand the equation and how to manipulate it, we encourage you to explore further. Research the applications of E=mc² in various fields, delve into the concepts of special and general relativity, and continue to ask questions about the universe around you. Share this knowledge with others, discuss its implications, and inspire the next generation of scientists and thinkers. Consider exploring simulations or interactive tools that demonstrate mass-energy equivalence. Your journey into the world of physics has just begun!
Latest Posts
Latest Posts
-
How Many Quarts Go Into A Pint
Nov 12, 2025
-
Rs 50 000 Crore In Dollars
Nov 12, 2025
-
What Is A Inclined Plane Used For
Nov 12, 2025
-
What Is A Storm Surge Simple Definition
Nov 12, 2025
-
How Long Do Glass Frogs Live
Nov 12, 2025
Related Post
Thank you for visiting our website which covers about E Equals Mc Squared Solve For M . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.