5 Out Of 50 As A Percentage
xcpfox
Nov 11, 2025 · 10 min read
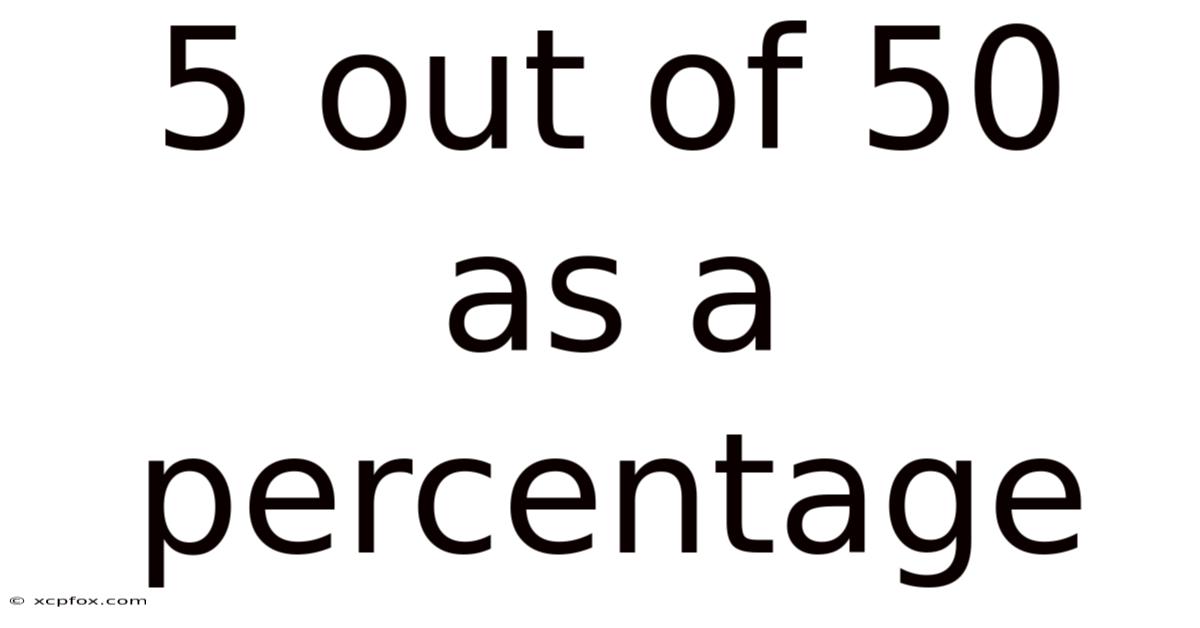
Table of Contents
Imagine you're at a school fair, and there's a raffle with 50 tickets in total. You bought 5 tickets, hoping to win that grand prize. What are your chances? How do you calculate your odds of success? Expressing this situation as a percentage helps you understand your probability in a clear and straightforward way. This is just one simple example of how calculating 5 out of 50 as a percentage can be useful in everyday life.
Whether you're calculating quiz scores, understanding survey results, or figuring out discounts at your favorite store, percentages are all around us. Learning to convert fractions like 5/50 into percentages unlocks a valuable skill that simplifies decision-making and helps you interpret data more effectively. In this article, we will dive deep into understanding how to accurately calculate 5 out of 50 as a percentage, and how this skill can be applied in various real-world scenarios.
Main Subheading
Understanding the concept of percentages is essential in various aspects of life, from calculating grades to analyzing financial data. A percentage is essentially a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "out of one hundred." Using percentages allows us to standardize comparisons, making it easier to understand proportions and ratios. When we talk about 5 out of 50 as a percentage, we're asking what portion of 100 this ratio represents.
Percentages are not just mathematical tools; they are integral to communication and decision-making. They provide a common ground for comparison, whether it's assessing the effectiveness of a marketing campaign or understanding the distribution of resources in a project. The ability to convert any fraction, including 5 out of 50, into a percentage is a fundamental skill. It equips you with the means to interpret information accurately and make informed decisions based on quantifiable data.
Comprehensive Overview
To truly understand how to calculate 5 out of 50 as a percentage, we need to break down the core concepts. The process involves a few simple steps that transform a ratio into a percentage. Here’s a detailed look at the mechanics:
-
Understanding the Fraction: The phrase "5 out of 50" represents a fraction, which is written as 5/50. The numerator (5) is the part, and the denominator (50) is the whole.
-
Converting the Fraction to a Decimal: To convert the fraction 5/50 into a decimal, you divide the numerator by the denominator. So, 5 ÷ 50 = 0.1.
-
Converting the Decimal to a Percentage: To convert a decimal to a percentage, you multiply the decimal by 100. In this case, 0.1 × 100 = 10%. Therefore, 5 out of 50 as a percentage is 10%.
This calculation provides a clear and easily understandable representation of the proportion. Now, let's delve deeper into the underlying principles.
The beauty of percentages lies in their universality. They provide a normalized way to express ratios, making it simple to compare different quantities. For instance, if you scored 5 out of 50 on a quiz, understanding that this is 10% gives you an immediate sense of your performance. If another student scored 20 out of 100, knowing that this is 20% makes it easy to compare your scores, even though the total possible scores were different.
The historical roots of percentages can be traced back to ancient Rome, where calculations were often made in terms of fractions of 100. As trade and commerce evolved, the need for a standardized way to express proportions became increasingly important. By the Middle Ages, percentages had become a common tool in financial calculations, and their use has only grown since then.
Moreover, the mathematical foundation of percentages is closely linked to the concept of proportionality. When we say that 5 out of 50 is 10%, we are stating that the ratio 5:50 is proportional to the ratio 10:100. This understanding is crucial for applying percentages accurately in various contexts. Whether you're calculating interest rates, discounts, or statistical probabilities, the underlying principle remains the same: expressing a part as a fraction of a whole, normalized to 100.
Trends and Latest Developments
In today's data-driven world, the use of percentages is more prevalent than ever. From business analytics to scientific research, percentages are used to summarize, analyze, and present data in a clear and understandable format. One of the latest trends is the increasing use of data visualization tools that automatically convert raw data into percentages and graphical representations. These tools make it easier for professionals to identify trends, patterns, and anomalies in large datasets.
According to recent studies, a significant percentage of business reports and academic papers include data presented as percentages. This highlights the ongoing importance of understanding how to calculate and interpret percentages accurately. Furthermore, with the rise of big data, there is a growing need for professionals who can analyze and communicate complex information using percentages.
Additionally, there has been a surge in online tools and calculators that simplify the process of converting fractions to percentages. These tools are particularly useful for individuals who need to perform quick calculations without manually dividing and multiplying. However, it's important to understand the underlying math to avoid blindly relying on these tools and to ensure the accuracy of the results.
Professional insights suggest that while technology can automate percentage calculations, a solid understanding of the concepts remains crucial. Professionals in finance, marketing, and research fields emphasize the importance of being able to critically evaluate data presented as percentages. This includes understanding the context in which the percentages are used, the sample sizes involved, and the potential for bias in the data.
Moreover, ethical considerations play a vital role in the use of percentages. It's important to present data accurately and avoid manipulating percentages to mislead or misrepresent information. Transparency and honesty are key principles in data analysis and communication. For example, when presenting survey results as percentages, it's essential to disclose the sample size and any limitations of the data.
Tips and Expert Advice
Calculating 5 out of 50 as a percentage might seem straightforward, but there are nuances and best practices that can enhance your understanding and application of this skill. Here are some tips and expert advice to help you master percentage calculations:
-
Double-Check Your Work: Always double-check your calculations to ensure accuracy. A small error in division or multiplication can lead to a significant difference in the final percentage.
- For example, if you mistakenly divide 5 by 5 instead of 5 by 50, you will get 1 instead of 0.1. This would result in a percentage of 100%, which is clearly incorrect.
-
Simplify Fractions First: Before converting a fraction to a percentage, simplify it to its lowest terms. This can make the calculation easier and reduce the chance of errors.
- In the case of 5/50, you can simplify it by dividing both the numerator and the denominator by 5, which gives you 1/10. Converting 1/10 to a decimal (1 ÷ 10 = 0.1) and then to a percentage (0.1 × 100 = 10%) is often simpler than working with the original fraction.
-
Understand the Context: Always consider the context in which you are using percentages. The same percentage can have different meanings depending on the situation.
- For example, a 10% increase in sales for a small business might be a significant achievement, while a 10% increase for a large corporation might be relatively minor.
-
Use Benchmarks: Use benchmarks to compare percentages and gain a better understanding of their significance.
- For instance, if you know that the average score on a test is 70%, you can compare your score of 10% (from the 5 out of 50 example) to this benchmark to understand how you performed relative to others.
-
Be Aware of Common Mistakes: Be aware of common mistakes, such as confusing percentages with percentage points or misinterpreting the base value.
- For example, if an interest rate increases from 5% to 7%, this is an increase of 2 percentage points, not a 2% increase. The actual percentage increase is (7-5)/5 = 40%.
-
Practice Regularly: The more you practice calculating percentages, the more comfortable and confident you will become. Use real-world examples to practice and apply your skills.
- Try calculating discounts at the store, figuring out tips at restaurants, or analyzing statistics from news articles.
-
Use Technology Wisely: While online calculators can be helpful, it's important to understand the underlying math. Use calculators as a tool to check your work, but don't rely on them exclusively.
- Make sure you understand how the calculator is performing the calculation and that you are entering the correct values.
FAQ
Q: What does it mean to express 5 out of 50 as a percentage?
A: Expressing 5 out of 50 as a percentage means determining what proportion of 100 the ratio 5/50 represents. In this case, it's 10%. This provides a standardized way to understand the proportion in relation to a whole.
Q: How do I convert 5 out of 50 to a percentage?
A: To convert 5 out of 50 to a percentage, divide 5 by 50 to get 0.1, then multiply 0.1 by 100. The result is 10%, so 5 out of 50 is equal to 10%.
Q: Why is it useful to know how to calculate percentages?
A: Calculating percentages is useful in many areas of life, including finance, education, retail, and statistics. It helps in understanding proportions, comparing values, and making informed decisions based on quantifiable data.
Q: Can I use a calculator to find the percentage?
A: Yes, you can use a calculator to find the percentage. Simply divide the part (5) by the whole (50) and then multiply by 100. However, understanding the underlying math is important to ensure you're using the calculator correctly.
Q: Is there a formula for calculating percentages?
A: Yes, the formula for calculating percentages is: (Part / Whole) × 100. In the case of 5 out of 50, it would be (5 / 50) × 100 = 10%.
Q: How can I practice calculating percentages?
A: You can practice calculating percentages by using real-world examples, such as figuring out discounts while shopping, calculating tips at restaurants, or analyzing statistics from news articles. The more you practice, the more confident you will become.
Conclusion
In summary, calculating 5 out of 50 as a percentage is a fundamental skill that offers valuable insights into proportions and ratios. The process involves converting the fraction to a decimal and then multiplying by 100, resulting in 10%. This skill is not only useful in academic settings but also in various real-world scenarios, from financial planning to data analysis. By mastering this skill, you enhance your ability to interpret information accurately and make informed decisions.
Now that you have a comprehensive understanding of how to calculate 5 out of 50 as a percentage, take the next step by applying this knowledge in your daily life. Whether it's calculating your savings rate, understanding survey results, or evaluating investment options, the ability to work with percentages will undoubtedly prove beneficial. Share this article with friends and colleagues to help them improve their understanding, and leave a comment below sharing how you plan to use this knowledge in your own life.
Latest Posts
Latest Posts
-
Conversion Of Mm To Inches Chart
Nov 11, 2025
-
Clever Way To Remember Photosynthesis Equation
Nov 11, 2025
-
How To Find Least Common Multiple Of 3 Numbers
Nov 11, 2025
-
How To Work Out Exterior Angles
Nov 11, 2025
-
What Does Fastidious Mean In Microbiology
Nov 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Out Of 50 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.