3 Times Square Root Of 3
xcpfox
Nov 13, 2025 · 10 min read
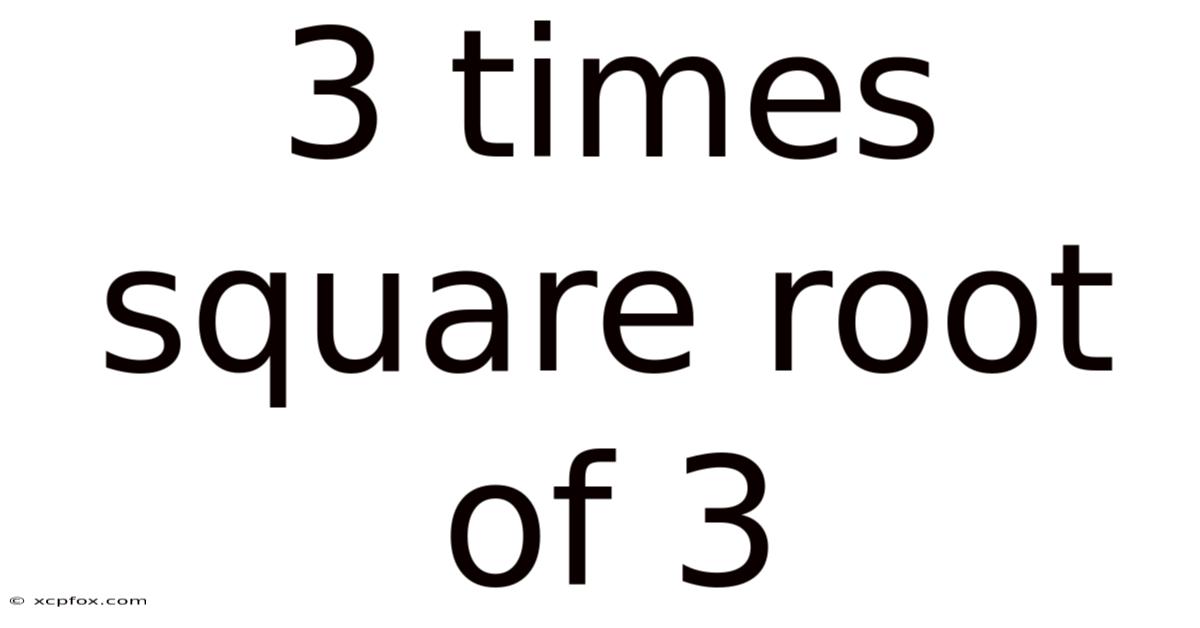
Table of Contents
The number 3 times square root of 3, often written as 3√3, might seem like a simple mathematical expression, but it carries a depth that touches upon various mathematical concepts and applications. From its basic arithmetic representation to its use in geometry, trigonometry, and even advanced calculus, understanding 3√3 unlocks a richer appreciation for mathematical principles. Let's explore this number in detail to understand its properties, applications, and significance.
Main Subheading
Mathematics, at its core, is about understanding numbers and their relationships. The number 3√3 is a fascinating example of how seemingly straightforward numbers can lead to complex and interesting mathematical investigations. To fully appreciate 3√3, we must first understand the basics: what it means to multiply a whole number by a square root, how the square root of 3 is derived, and why such expressions are useful. Combining a rational number (3) with an irrational number (√3) creates a unique value that appears surprisingly often in geometric and algebraic contexts.
Comprehensive Overview
Understanding the Basics
The expression 3√3 is a product of two numbers: 3 and √3. The number 3 is an integer, a basic counting number. The number √3 is the square root of 3, which means it's the number that, when multiplied by itself, equals 3. Mathematically, √3 * √3 = 3. The square root of 3 is an irrational number, meaning it cannot be expressed as a simple fraction (a/b, where a and b are integers). Its decimal representation goes on infinitely without repeating: √3 ≈ 1.7320508...
The Square Root of 3
The square root of 3 is more than just a number; it's a fundamental constant in mathematics. It arises naturally in various geometrical problems, particularly those involving equilateral triangles and regular hexagons. For instance, in an equilateral triangle with side length 2, the altitude (height) from one vertex to the midpoint of the opposite side is √3. This direct geometric connection underscores the importance of √3 in spatial relationships.
Irrational Numbers and Their Significance
Irrational numbers like √3 play a crucial role in completing the number line. If we only had rational numbers, there would be "gaps" in our understanding of quantity and measurement. Irrational numbers fill these gaps, allowing for precise measurements and calculations in fields like physics, engineering, and computer science. They remind us that not all numbers can be neatly expressed as ratios, adding depth to our understanding of numerical systems.
Arithmetic Operations with 3√3
When working with 3√3, basic arithmetic operations follow specific rules. For example, adding or subtracting terms involving √3 requires combining like terms:
- 2√3 + 3√3 = 5√3
- 5√3 - 2√3 = 3√3
Multiplying or dividing by constants is straightforward:
- 2 * (3√3) = 6√3
- (3√3) / 3 = √3
When multiplying two terms involving square roots, the rules change slightly:
- (3√3) * (2√3) = 6 * (√3 * √3) = 6 * 3 = 18
Representation and Approximation
While 3√3 is a precise value, it's often useful to approximate it for practical purposes. Since √3 ≈ 1.7320508..., we can approximate 3√3 as: 3 * 1.7320508... ≈ 5.1961524...
This approximation is accurate to several decimal places and is sufficient for most engineering and scientific calculations. For higher precision, one can use more decimal places of √3 or computational tools that retain the exact symbolic representation.
Algebraic Context
In algebra, 3√3 can appear as a solution to equations or as a coefficient in expressions. For example, consider the equation x² = 27. Taking the square root of both sides gives x = ±√27. Simplifying √27 gives √(9 * 3) = √(9) * √(3) = 3√3. Therefore, the solutions to the equation x² = 27 are x = 3√3 and x = -3√3.
Geometric Applications
The number 3√3 appears in various geometric contexts. We already mentioned its relation to equilateral triangles, but it also shows up in the geometry of regular hexagons. A regular hexagon can be divided into six equilateral triangles. If each side of the hexagon has length 1, the distance from the center to any vertex is also 1, and the distance across the hexagon (through the center) is 2. However, consider a hexagon made of equilateral triangles with sides of length √3. In this case, the distance from the center to any vertex is √3, and multiplying this by three for a related calculation gives us 3√3.
Trigonometric Connections
In trigonometry, 3√3 can appear in the context of special angles and their trigonometric ratios. While not a direct output of common angles like 30°, 45°, or 60°, it can arise in related calculations or in more complex geometrical setups that involve trigonometric functions.
Advanced Applications
In more advanced mathematics, such as calculus and complex analysis, 3√3 can appear in the context of limits, series, and integrals. It might arise as a value in a definite integral or as part of a series expansion. For example, in some complex number problems, geometric interpretations can lead to expressions involving √3, and subsequently, 3√3.
Trends and Latest Developments
While 3√3 is a fixed mathematical value, its relevance and applications continue to evolve with advances in computational mathematics and applied sciences. Here are a few notable trends and developments:
Computational Mathematics
With the rise of computer algebra systems (CAS) like Mathematica, Maple, and SageMath, the exact representation and manipulation of numbers like 3√3 have become more accessible. These tools allow researchers and engineers to perform complex calculations without relying solely on numerical approximations, preserving the integrity of mathematical expressions.
Data Science and Analytics
In data science, geometric and spatial data analysis often involves calculations with irrational numbers. For example, determining distances and areas in geographic information systems (GIS) can lead to expressions involving √3 and its multiples. The increasing use of spatial data in urban planning, environmental science, and logistics means that understanding and efficiently computing with these numbers is more important than ever.
Physics and Engineering
In physics, particularly in areas like quantum mechanics and materials science, calculations involving crystal structures and wave functions often involve irrational numbers like √3. These calculations can become incredibly complex, and efficient computation and manipulation of expressions involving 3√3 are crucial for accurate modeling and simulation.
Education and Outreach
There is a growing emphasis on mathematical literacy and making mathematical concepts accessible to a broader audience. Educational resources and outreach programs often use examples like 3√3 to illustrate the beauty and utility of mathematics in everyday life. By showing how these numbers arise naturally in geometry and other applications, educators can help students develop a deeper appreciation for the subject.
Interdisciplinary Research
The application of mathematical principles in interdisciplinary research is also driving interest in numbers like 3√3. For example, in mathematical biology, models of population dynamics or ecological systems can involve geometric considerations that lead to expressions involving √3. Similarly, in mathematical finance, geometric models of market behavior might utilize these numbers.
Tips and Expert Advice
Understanding and working with 3√3 can be made easier with a few practical tips and expert advice:
Master the Fundamentals
Before diving into complex applications, ensure you have a solid understanding of the fundamental concepts:
- Understand Square Roots: Know what a square root is and how to calculate it (both manually and with a calculator).
- Rational vs. Irrational Numbers: Grasp the difference between rational and irrational numbers, and why irrational numbers are essential.
- Arithmetic Operations: Practice adding, subtracting, multiplying, and dividing expressions involving square roots.
Use Approximations Wisely
While it's essential to understand the exact value of 3√3, approximations are often necessary for practical calculations. When using approximations:
- Know Your Precision: Be aware of the level of precision required for your application.
- Use Calculators and Software: Utilize calculators or software that can handle irrational numbers and provide accurate approximations.
- Round Appropriately: Round your final answer to the appropriate number of significant figures.
Visualize Geometric Connections
One of the best ways to understand 3√3 is to visualize its geometric connections:
- Equilateral Triangles: Draw equilateral triangles and calculate their heights to see √3 in action.
- Regular Hexagons: Explore the geometry of regular hexagons and their relationship to equilateral triangles.
- 3D Shapes: Extend these concepts to 3D shapes, such as tetrahedra and octahedra, which also involve √3 in their measurements.
Leverage Technology
Take advantage of technology to explore and manipulate expressions involving 3√3:
- Computer Algebra Systems: Use CAS software like Mathematica, Maple, or SageMath to perform symbolic calculations.
- Online Calculators: Use online calculators that can handle irrational numbers and provide accurate approximations.
- Spreadsheets: Employ spreadsheet software like Excel or Google Sheets to perform calculations and create visualizations.
Practice Problem Solving
The best way to master 3√3 is to practice solving problems that involve it:
- Algebraic Equations: Solve equations that have solutions involving 3√3.
- Geometric Problems: Tackle geometric problems that require calculating lengths, areas, or volumes using 3√3.
- Real-World Applications: Look for real-world applications in physics, engineering, or other fields and try to model them mathematically.
Understand Context
Always consider the context in which 3√3 appears:
- Units: Pay attention to units of measurement and ensure your calculations are consistent.
- Assumptions: Be aware of any assumptions you are making in your calculations and how they might affect the accuracy of your results.
- Limitations: Recognize the limitations of your model or calculations and be cautious about over-interpreting your results.
Seek Expert Guidance
Don't hesitate to seek guidance from experts when needed:
- Teachers and Professors: Ask your teachers or professors for help if you are struggling with a concept.
- Online Forums: Participate in online forums and communities where you can ask questions and get advice from experienced mathematicians.
- Tutoring: Consider hiring a tutor who can provide personalized instruction and help you master the material.
FAQ
Q: What is the exact value of 3√3? A: 3√3 is the exact value. It represents 3 times the square root of 3. Since √3 is an irrational number, its decimal representation is non-repeating and non-terminating, so 3√3 also has a non-repeating, non-terminating decimal representation.
Q: How can I approximate 3√3? A: To approximate 3√3, you can use the approximation √3 ≈ 1.732. Therefore, 3√3 ≈ 3 * 1.732 = 5.196.
Q: Where does 3√3 commonly appear in mathematics? A: 3√3 commonly appears in geometry, particularly in problems involving equilateral triangles, regular hexagons, and other geometric figures that have connections to the square root of 3. It also appears in algebraic solutions and trigonometric calculations.
Q: Can 3√3 be simplified further? A: No, 3√3 is already in its simplest form. The number 3 is a rational number, and √3 is an irrational number. They cannot be combined further into a simpler algebraic expression.
Q: Is 3√3 a rational or irrational number? A: 3√3 is an irrational number. Multiplying a rational number (3) by an irrational number (√3) results in an irrational number.
Q: How do I perform arithmetic operations with 3√3? A: When performing arithmetic operations:
- Addition/Subtraction: Combine like terms, e.g., 2√3 + 3√3 = 5√3.
- Multiplication: Multiply the coefficients and the square roots separately, e.g., 2 * (3√3) = 6√3 and (3√3) * (2√3) = 6 * 3 = 18.
- Division: Divide the coefficients, e.g., (3√3) / 3 = √3.
Conclusion
The number 3√3, while seemingly simple, embodies deep mathematical concepts ranging from basic arithmetic to advanced applications in geometry, trigonometry, and beyond. Understanding its properties, applications, and the techniques for working with it enhances our appreciation for the interconnectedness of mathematics. By mastering the fundamentals, visualizing geometric connections, and leveraging technology, you can confidently tackle problems involving 3√3 and similar mathematical expressions. Keep exploring, practicing, and seeking expert guidance to deepen your mathematical understanding and skills. Ready to delve further? Try applying 3√3 in geometric constructions or algebraic problem-solving to solidify your grasp of this fascinating number.
Latest Posts
Latest Posts
-
What Is Equivalent Fraction To 1 3
Nov 13, 2025
-
What Is The Purpose Of The Cornea
Nov 13, 2025
-
Iv Organic 3 In 1 Plant Guard
Nov 13, 2025
-
How Are Humans Disrupting The Carbon Cycle
Nov 13, 2025
-
Area And Perimeter Of Shapes Formula
Nov 13, 2025
Related Post
Thank you for visiting our website which covers about 3 Times Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.